Data Privacy and Security

Machine learning models are sometimes trained on sensitive data, such as healthcare records, and often times, these models are made publicly available, even though the data they are trained on is sensitive and not suitable for release. The model architecture/weights might be made available for download, or the model might be deployed as an inference endpoint, available for anyone to make predictions on any data in a black-box way.

A natural question arises: do these public models leak private information about the data on which they are trained? It turns out that they do, and this gives rise to a variety of attacks on ML models, including:

There are many other types of attacks on data / ML models, including adversarial examples (Szegedy et al., 2013), data poisoning attacks (Chen et al., 2017), model inversion attacks (Fredrikson et al., 2014), and model extraction attacks (Tramèr et al., 2016). ML security is an active area of research, and there are many thousands of papers on the topic, as well as recently-discovered issues like prompt injection in LLMs that haven’t even received a systematic treatment from researchers yet.

This lecture covers security-oriented thinking in the context of machine learning, and it focuses on inference and extraction attacks. Finally, it touches on defenses against privacy attacks, including empirical defenses and differential privacy.

Defining security: security goals and threat models

Security is not a set of practices to follow, it is a way of thinking.

To be able to reason about whether a system is secure, you must first define:

Once these are defined, then you can decide whether a system is secure by thinking about whether any possible adversary (that follows the threat model) could violate the security goal of your system. Only if the answer is “no” is the system secure.

Quantifying over all adversaries is one aspect of what makes security challenging, and why it’s important to specify good threat models (without sufficiently constraining the adversary, most security goals cannot be achieved).

For any given system, fully specifying a security goal and threat model can require a lot of thought. Let’s build some intuition by doing some threat modeling.

Image prediction API

Google Cloud Vision prediction

Consider a cloud-based image prediction API like the Google Cloud Vision API, which takes in an image and returns a prediction of labels and associated probabilities. A security goal might include that an attacker should not be able to extract the ML model. The model is proprietary, and collecting a large dataset and training a model is expensive, so a cloud provider might not want an adversary to be able to extract model architecture/weights. In threat modeling, the cloud provider might assume that the adversary can:

Even black-box is a spectrum: probabilities for all labels, probabilities for top-5 labels, top-5 predictions in sorted order, top-1 probability, top-1 prediction, ...

The cloud provider might assume that the adversary can’t:

Patient risk prediction model

Suppose that a hospital trained an ML model on patient data to predict the likelihood of the patient needing intensive care, and the hospital made the model publicly available for download, so that other hospitals as well as researchers could use it. A security goal might include that the model should not reveal any private information about any patient who was treated at the hospital. For example, given a particular patient, an adversary should not be able to tell whether that patient was in the training dataset of the model. The hospital might assume that the adversary can:

The hospital might assume that the adversary can’t:

Membership inference attacks

Membership inference attacks determine whether a data point is in the training set of an ML model. Consider an ML model $M$ trained on a dataset $D$ of data points $(\mathbf{x}_i, y_i)$, where $M$ produces probability distributions over the set of labels, $M : \mathbf{x} \rightarrow \mathbf{y}$. The goal of a membership inference attack is to determine whether a data point $(\mathbf{x}, y)$ is in the training set of $M$, i.e., whether $(\mathbf{x}, y) \in D$, given access to $M$.

Different attacks consider different settings where the adversary has varying access to $M$. In this lecture, we focus on black-box access: the attacker has the ability to query $M$ for attacker-chosen inputs, and the attacker obtains the model output (e.g., predicted probabilities for all classes).

Shadow training (Shokri et al., 2016)

This attack uses machine learning to break the privacy of machine learning, by training a model to infer whether or not a data point is in the training set of the target model. The approach trains an attack model $A$ that takes in a data point’s class label $y$ and a target model’s output $\mathbf{y}$ and performs binary classification, whether or not the data point is in the training set: $A : (y, \mathbf{y}) \rightarrow \{\mathrm{in}, \mathrm{out}\}$. It collects a training dataset for this attack model with a collection of “shadow models”.

Step 1: collecting training data

The attack assumes that the attacker has access to additional data $D_{\mathrm{shadow}}$ that fits the format of the target model. For example, if the target model is an image classifier, then the attacker needs to have access to a bunch of images. The attack trains “shadow models” on this dataset to produce training data for the attack model.

  1. Partition the dataset $D_{\mathrm{shadow}}$ into a $D_{\mathrm{in}}$ set and $D_{\mathrm{out}}$ set
  2. Choose a model architecture and train a shadow model $M_{\mathrm{shadow}}$ on $D_{\mathrm{in}}$
  3. For each $(\mathbf{x}, y) \in D_{\mathrm{in}}$, compute $\mathbf{y} = M_{\mathrm{shadow}}(\mathbf{x})$, the model’s output on $\mathbf{x}$, and use that to create a training data point $((y, \mathbf{y}), \mathrm{in})$.
  4. For each $(\mathbf{x}, y) \in D_{\mathrm{out}}$, compute $\mathbf{y} = M_{\mathrm{shadow}}(\mathbf{x})$, the model’s output on $\mathbf{x}$, and use that to create a training data point $((y, \mathbf{y}), \mathrm{out})$.

This process can be repeated many times, using different partitionings of $D_{\mathrm{shadow}}$ and different shadow models to create a large training dataset we call $D_{\mathrm{inout}}$.

Step 2: train the attack model

Next, the attack trains a binary classifier $A$ on $D_{\mathrm{inout}}$. You can use any classification algorithm for $A$; one possible choice is a multi-layer perceptron.

Step 3: perform the attack

Now, given a new data point $(\mathbf{x}, y)$, the attack computes $\mathbf{y} = M(\mathbf{x})$ by feeding the data point to the black-box target model $M$, and then predicts whether the data point is in the training set by evaluating $A(y, \mathbf{y})$.

Metrics-based attacks

Unlike attacks based on training a binary classifier, metric-based attacks are a lot more simple to implement and computationally inexpensive.

Prediction correctness based attack (Yeom et al., 2017)

Given a data point $(\mathbf{x}, y)$, this simple heuristic returns $\mathrm{in}$ if the model’s prediction $M(\mathbf{x})$ is correct (equal to $y$).

Intuition: this exploits the gap between train and test accuracy, where the model will likely correctly classify most or all of its test data but a much smaller fraction of training data.

Prediction loss based attack (Yeom et al., 2017)

This approach assigns a score to a data point $(\mathbf{x}, y)$ using the model’s loss for that particular data point, $L(M(\mathbf{x}), y)$. The score can be converted into a binary label $\mathrm{in}$ / $\mathrm{out}$ by thresholding at some chosen threshold $\tau$, outputting $\mathrm{in}$ if the loss is below the threshold.

For this metric, one way to choose a threshold might be to use the average or maximum loss of the model on the training data (which might be reported by the publisher of the model).

Intuition: this exploits the property that models are trained to minimize loss, and they can often achieve zero loss for training data.

Prediction confidence based (Salem et al., 2018)

This approach assigns a score to a data point based on the model’s confidence in its predicted class, $\max(M(\mathbf{x}))$. One way to choose a threshold would be to use the model’s average or minimum confidence on the training data, if available.

Intuition: this exploits the property that models are often more confident about the predictions for training data (even when that prediction doesn’t match the true label of the data point).

Prediction entropy based (Salem et al., 2018)

This approach assigns a score to a data point based on the entropy $H(\mathbf{y})$ of the model’s output, $\mathbf{y} = M(\mathbf{x})$:

\[ H(\mathbf{y}) = - \sum_{i} \mathbf{y}[i] \cdot \log \left( \mathbf{y}[i] \right) \]

Intuition: similar to the above, this exploits the property that models are often more confident about predictions for training data.

Data extraction attacks

Extraction attacks extract training data directly from a trained model. Neural networks unintentionally memorize portions of their input data (Carlini et al., 2019), and there are techniques for extracting this data, for example, from large language models (Carlini et al., 2021).

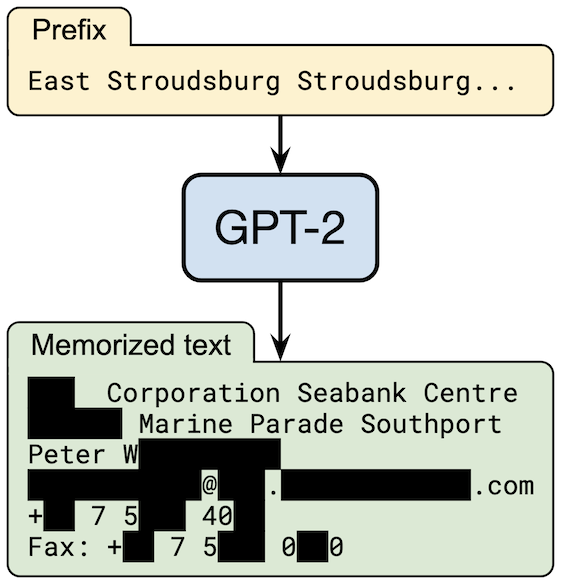
Data extraction attack against GPT-2

This is a real-world example. Some text is obscured to protect the victim's privacy.

At its core, the attack works as follows:

  1. Sample many sequences from the model. These are sampled by initializing the model with a start-of-sentence token and repeatedly sampling in an autoregressive fashion.
  2. Perform a membership inference attack to determine which generated sequences were likely part of the training set. A simple membership inference attack uses the perplexity of a sequence to measure how well the LLM “predicts” the tokens in that sequence. Given a model $\hat{p}$ that predicts the probability of the next token and sequence of tokens $x_1, x_2, \ldots, x_n$, the perplexity is:

\[ \mathcal{P} = \exp \left( - \frac{1}{n} \sum_{i = 1}^{n} \log \hat{p}\left( x_i \mid x_1, \ldots, x_{i-1} \right) \right) \]

The more refined version of this basic attack, presented in Carlini et al., 2021, is successful in extracting hundreds of memorized examples from GPT-2.

Defending against privacy leaks: empirical defenses and evaluation

There are a variety of ideas for defenses against privacy attacks that seem plausible. For example, to defend against membership inference attacks, the following techniques sound like reasonable ideas to try:

Many such ideas have been proposed, and many such ideas do not work. How might we break some of the ideas proposed above?

Security, especially with empirical solutions, can be a cat-and-mouse game. How should one evaluate a proposed defense?

Evaluating defenses

A first step is to fix the security goal, threat model, and evaluation metric (e.g., for a model inference attack, one might evaluate an attack based on the F1 score).

When evaluating an empirical defense, it’s important to keep Kerckhoffs’s principle in mind: a defense should be secure even if the adversary has knowledge about the defense. The opposite of this is “security through obscurity.”

For a defense to be secure, it must be robust (i.e., the system must satisfy its security goals) for all possible attacks within the threat model. Usually, in an evaluation, it’s not actually possible to quantify over all possible attacks. For this reason, in practice, we evaluate defenses by putting on the hat of an attacker and trying as hard as possible to break them. Only if we fail do we conclude that the defense might be a good one.

Towards a solution: differential privacy

For the issue of data privacy in machine learning, one promising approach that avoids the cat-and-mouse game of empirical defenses involves differential privacy (DP) (Dwork et al., 2006).

At a high level, DP is a definition of privacy that constrains how much an algorithm’s output can depend on individual data points within its input dataset. A randomized algorithm $\mathcal{A}$ operating on a dataset $\mathcal{D}$ is $(\epsilon, \delta)$-differentially private if:

\[ \mathrm{Pr}[\mathcal{A}(\mathcal{D}) \in S] \le \exp(\epsilon) \cdot \mathrm{Pr}[\mathcal{A}(\mathcal{D}’) \in S] + \delta \]

for any set $S$ of possible outputs of $\mathcal{A}$, and any two data sets $\mathcal{D}$, $\mathcal{D}’$ that differ in at most one element.

In the context of ML, the algorithm $\mathcal{A}$ is the model training algorithm, the input is the dataset $\mathcal{D}$, and the output of the algorithm, which is in $S$, and constrained by the definition of DP, is the model.

A differentially-private training algorithm (like DP-SGD, Abadi et al., 2016) ensures that the result (a trained model) does not change by much if a data point is added or removed, which intuitively provides some sort of privacy: the model can’t depend too much on specific data points.

There are challenges with applying DP in practice. One challenge is that the definition of DP includes two parameters, $\epsilon$ and $\delta$, that can be hard to set. Applied to a particular dataset, it can be hard to understand exactly what these parameters mean in terms of real-world privacy implications, and sometimes, choices of $\epsilon$ and $\delta$ that are good for privacy result in low-quality results (e.g., a model with poor performance).

Resources

Lab

The lab assignment for this lecture is to implement a membership inference attack. You are given a trained machine learning model, available as a black-box prediction function. Your task is to devise a method to determine whether or not a given data point was in the training set of this model. You may implement some of the ideas presented in today’s lecture, or you can look up other membership inference attack algorithms.

The lab assignments for the course are available in the dcai-lab repository.

Remember to run a git pull before doing every lab, to make sure you have the latest version of the labs.

The lab assignment for this class is in Lab - Membership Inference.ipynb.

Edit this page.

Licensed under CC BY-NC-SA.